STL 简介
每一个版本的 C++ 标准不仅规定了 C++ 的语法、语言特性,还规定了一套 C++ 内置库的实现规范,这个库便是 C++ 标准库。C++ 标准库中包含大量常用代码的实现,如输入输出、基本数据结构、内存管理、多线程支持等。
STL 即标准模板库(Standard Template Library),是 C++ 标准库的一部分,里面包含了一些模板化的通用的数据结构和算法。由于其模板化的特点,它能够兼容自定义的数据类型,合理利用 STL 可以避免编写无用算法,省去大量的造轮子的工作。
STL 标准模板库从广义上讲分为 算法(Algorithm)、容器(Container)及 迭代器(Iterator)3 类。
算法(Algorithm)
在头文件 <algorithm> 中,封装好了许多可直接调用的常用操作的函数,例如排序 sort() ,二分查找 binary_search() 。
算法作用于容器,它提供了对容器内容进行初始化、排序、搜索和转换等常用操作的实现方式,使用 STL 中的算法就不必自己造轮子了。
常用算法
元素相关
求最小值:min(x, y)
求两个元素的最小值。
求最大值:max(x, y)
求两个元素的最大值。
交换元素:swap(x, y)
交换两个元素。
示例程序
int a = 55, b = 23;
printf("min: %d\n", min(a, b)); // min: 23
printf("max: %d\n", max(a, b)); // max: 55
swap(a, b);
printf("After swap: a = %d, b = %d\n", a, b);
// After swap: a = 23, b = 55
区间相关
注:begin 表示区间起点,end 表示区间终点,区间为左闭右开 (端点 >= begin 且 < end)。例如示例程序区间,begin 为 a (数组名也表示数组首元素地址),end 为 a + 15(有 15 个数)。
int a[20] = {0, 1, 1, 2, 3, 5, 0, 7,
6, 9, 6, 0, 3, 5, 8};
查找:find(begin, end, x)
返回区间 [begin,end) 中第 1 个值为 x 的元素地址。
若不存在值为 x 的元素查找失败,则返回 end(终点地址)。
int *p = find(a, a + 15, 8); // p 存查找后的返回地址
if(p != a + 15) // 不是尾地址,则有找到
cout << find(a, a + 15, 6) - a; // 返回地址值减首地址就是下标
else
cout << "not found";
计数:count(begin, end, x)
统计区间 [begin,end) 种值为 x 的元素数量,返回值为整数。
printf("cnt(3): %d\n", count(a, a + 15, 3)); // 2
printf("cnt(0): %d\n", count(a, a + 15, 0)); // 3
printf("cnt(4): %d\n", count(a, a + 15, 4)); // 0
翻转:reverse(begin, end)
翻转区间 [begin,end) 中的元素序列。
reverse(a, a + 10); // 翻转 a[0] ~ a[9]
for(int i = 0; i < 15; i++) cout << a[i] << " ";
cout << "\n";
// 前 10 个元素变成:9 6 7 0 5 3 2 1 1 0,后 5 个不变
填充:fill(begin, end, x)
将区间 [begin,end) 中的每个元素值都设置为 x。
fill(a, a + 10, 3); // 将 a[0] ~ a[9] 都设为 3
for(int i = 0; i < 15; i++) cout << a[i] << " ";
cout << "\n";
// 输出:3 3 3 3 3 3 3 3 3 3 6 0 3 5 8
排序相关
排序:sort(begin, end, compare)
begin 和 end 分别为待排序数组的首地址和尾地址;compare 表示排序的比较函数,可省略不填。
默认为升序,若要降序,可在第三个参数处填入 greater<int>()。
sort 排序采用的是成熟的“快速排序算法”,可以保证很好的平均性能,其时间复杂度为 nlog(n)。
稳定排序:stable_sort (begin, end, compare)
stable_sort() 能保持相等元素的相对顺序在排序前后一致。即使原来相同的值在序列中的相对位置不变。例如初始序列中有两个元素 A 和 B 的值相等,且 A 排在 B 的前面,排序后 A 仍然排在 B 的前面,这种排序叫作稳定排序。
去重:unique(begin, end)
将区间 [begin,end) 中的连续相同元素进行去重,返回去重后的尾指针。
不连续的相同元素不会被压缩去重,因此一般先排序后去重。
示例程序
sort(a, a + 15); // 对 a[0] ~ a[14] 元素排序
int k = unique(a, a + 15) - a; // 对连续相同元素去重,减 a 去重后元素个数
printf("distinct numbers: %d\n", k); // distinct numbers: 9
for(int i = 0; i < k; i++) cout << a[i] << " ";
// 输出:0 1 2 3 5 6 7 8 9
cout << "\n";
sort(a, a + k, greater<int>()); // greater<>() 表示降序排序
for(int i = 0; i < k; i++) cout << a[i] << " ";
// 输出:9 8 7 6 5 3 2 1 0
cout << "\n";
二分查找
注:begin 表示区间起点,end 表示区间终点,区间为左闭右开 (端点 >= begin 且 < end)。
二分查找:binary_search(begin, end, x)
判断 x 是否在 [begin,end) 里,如果存在则返回 true,否则返回 false。
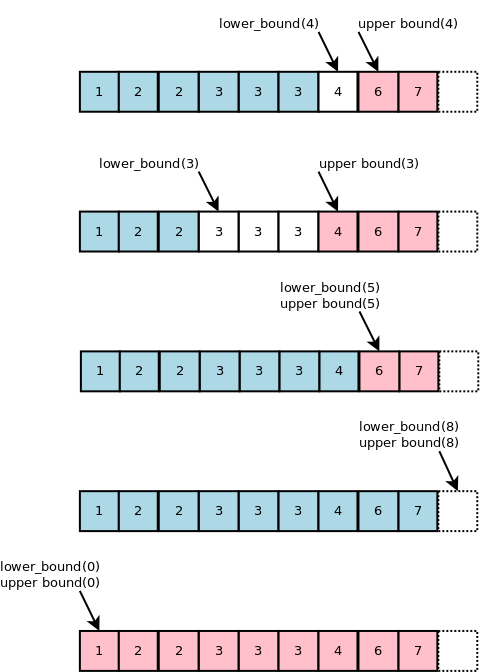
查找左边界:lower_bound(begin, end, x)
在一个有序序列 [begin,end) 中进行二分查找,返回第一个 大于等于 x 的元素的地址。
如果区间内所有元素都小于 x,则返回 end 的地址,且 end 的地址是越界的。
查找右边界:upper_bound(begin, end, x)
在一个有序序列 [begin,end) 中进行二分查找,返回第一个 大于 x 的元素的地址。
如果区间内所有元素都小于 x,则返回 end 的地址,且 end 的地址是越界的。
图解
特别注意
- lower_bound 和 upper_bound 二分查找的区间必须为有序序列。
- 由于 lower_bound 和 upper_bound 返回的是数组元素的地址值,所以用它减去数组首地址的值就是该数组元素的下标,即 lower/upper_bound(a, a + n, x) – a 可以表示查找到的下标。
- 降序序列使用要注意以下两点:
- lower_bound 的正确写法为 lower_bound(begin, end, x, greater<int>()),或类似于 sort 排序,使用自定义比较函数。若 x 在序列中,则返回 x 第一次出现的位置,否则返回第一个插入 x 不影响原序列顺序的位置。
- upper_bound 的正确写法为 upper_bound(begin, end, x, greater<int>()),或类似于 sort 排序,使用自定义比较函数。若 x 在序列中,则返回第一个小于 x 的位置,否则返回第一个插入 x 不影响原序列顺序的位置。
排列
下个排列:next_permutation(begin, end)
将当前排列更改为全排列中的下一个排列。
注:如果当前排列已经是全排列中的最后一个排列(元素完全从大到小排列),函数返回 false,并将排列更改为全排列中的第一个排列(元素完全从小到大排列);否则,函数返回 true。
上个排列:pre_permutation(begin, end)
将当前排列更改为全排列中的上一个排列。用法同 next_permutation()。
经典例题
Bookshelf B
思路
使用 sort(a, a + n, greater<int>()) 逆序排序
代码
#include <bits/stdc++.h>
using namespace std;
int n, h[20005], s, b, i;
int main(){
scanf("%d %d", &n, &b);
for(int i = 1; i <= n; i++)
scanf("%d", &h[i]);
sort(h + 1, h + 1 + n, greater<int>());
for(i = 1; s < b; i++)
s += h[i]; // 循环结束时 i 为第一个不满足条件处
printf("%d", --i);
return 0;
}
不重复地输出数
思路
使用 sort() 和 unique()
代码
#include <bits/stdc++.h>
using namespace std;
int n, a[100005];
int main(){
scanf("%d", &n);
for(int i = 0; i < n; i++)
scanf("%d", &a[i]);
sort(a, a + n);
// 返回去重后最后一个元素地址,减首地址为元素个数
int k = unique(a, a + n) - a;
for(int i = 0; i < k; i++)
printf("%d ", a[i]);
return 0;
}
查找
思路
使用 lower_bound()
代码
#include <bits/stdc++.h>
using namespace std;
int n, m, a[1000005], q;
int main(){
scanf("%d %d", &n, &m);
for(int i = 0; i < n; i++){
scanf("%d", &a[i]);
}
while(m--){
scanf("%d", &q);
int p = lower_bound(a, a + n, q) - a;
if(a[p] == q)
printf("%d ", p + 1);
else
printf("-1 ");
}
return 0;
}
和为给定数
思路
使用 lower_bound()
代码
#include <bits/stdc++.h>
using namespace std;
int n, a[100005], m;
int main(){
scanf("%d", &n);
for(int i = 0; i < n; i++){
scanf("%d", &a[i]);
}
scanf("%d", &m);
sort(a, a + n);
for(int i = 0; i < n; i++){
// [i+1, n-1] 查找 m - a[i]
int j = lower_bound(a + i + 1, a + n, m - a[i]) - a;
if(a[i] + a[j] == m){
printf("%d %d\n", a[i], a[j]);
return 0;
}
}
printf("No");
return 0;
}
A-B 数对
思路
使用 lower_bound() / upper_bound()
代码
#include <bits/stdc++.h>
using namespace std;
int n, a[200005], c;
long long s;
int main(){
scanf("%d %d", &n, &c);
for(int i = 0; i < n; i++){
scanf("%d", &a[i]);
}
sort(a, a + n);
for(int i = 0; i < n; i++){ // 枚举较小数 a[i]
// 在 i 后面 [i + 1, n) 查找较大数 a[i] + c
int t = upper_bound(a + i + 1, a + n, a[i] + c) // 第一个大于 a[i] + c
- lower_bound(a + i + 1, a + n, a[i] + c); // 第一个大于等于 a[i] + c
s += t;
}
printf("%lld", s);
return 0;
}
全排列问题
思路
使用 next_permutation()
代码
#include <bits/stdc++.h>
using namespace std;
int n, a[10005];
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i++)
a[i] = i;
do{
for(int i = 1; i <= n; i++)
printf("%5d ", a[i]);
printf("\n");
}while(next_permutation(a + 1, a + 1 + n));
return 0;
}
火星人
思路
使用 next_permutation()
代码
#include <bits/stdc++.h>
using namespace std;
int n, m, a[10005];
int main(){
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%d", &a[i]);
while(m--){ // 循环 m 次生成 a[] 的下个排列
next_permutation(a + 1, a + 1 + n);
}
for(int i = 1; i <= n; i++)
printf("%d ", a[i]);
return 0;
}
数组元素循环右移问题
思路
使用 reverse()。循环移位 m 位的三次翻转算法:
- 翻转 a(1)……a( n- m)
- 翻转 a(n – m + 1)……a(n)
- 翻转 a(1) ~ a(n)
#include <bits/stdc++.h>
using namespace std;
int n, a[105], m;
int main(){
cin >> n >> m;
m %= n; // 移位大于 n 的情况
for(int i = 1; i <= n; i++)
cin >> a[i];
reverse(a + n - m + 1, a + 1 + n); // 翻转右半部分
reverse(a + 1, a + n - m + 1); // 翻转左半部分
reverse(a + 1, a + 1 + n); // 整体再翻转
for(int i = 1; i <= n; i++)
cout << a[i] << (i < n ? " " : "");
return 0;
}
导弹拦截
思路
先假设都使用系统 1,对每颗导弹根据到系统 1 的距离从小到大排序,再尝试加入系统 2,枚举所有可能的点计算总距,取所有方案中的最小值。
代码
#include <bits/stdc++.h>
using namespace std;
struct B{
int d1, d2;
};
bool cmp(B b, B c){ // 第一套系统距离小到大排序
return b.d1 < c.d1;
}
int main(){
B a[100005];
int x_1, y_1, x_2, y_2, x, y, n;
scanf("%d %d %d %d %d", &x_1, &y_1, &x_2, &y_2, &n);
for(int i = 1; i <= n; i++){
scanf("%d %d", &x, &y);
a[i].d1 = pow(x - x_1, 2) + pow(y - y_1, 2); // 系统 1 距离
a[i].d2 = pow(x - x_2, 2) + pow(y - y_2, 2); // 系统 2 距离
}
sort(a + 1, a + 1 + n, cmp);
// 求 a[i].d2 的后缀最大值
a[0].d1 = 0; // 初始化系统 1 不用的情况
int max_d2 = 0, mins = a[n].d1; // 全用系统 1
for(int i = n; i >= 1; i--){ // 从 a[i ~ n] 用系统 2
max_d2 = max(max_d2, a[i].d2); // a[i ~ n] 中的 d2 最大值
// 算总距:a[1] ~ a[i-1] 系统 1 拦, a[i] ~ a[n] 系统 2 拦
mins = min(mins, a[i-1].d1 + max_d2);
}
printf("%d", mins);
return 0;
}
